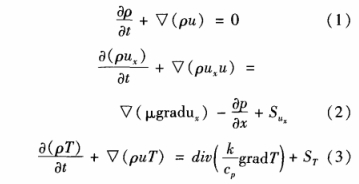摘要:基于(yú)渦街理論(lun),分别對圓(yuán)形阻流體(tǐ)、正方形阻(zu)流體和三(sān)👣角形阻流(liu)體所形成(cheng)的渦街場(chǎng)進行仿真(zhen)🐇研究,同時(shí)✍️對三種阻(zu)流體對應(yīng)的渦街流(liú)量計 進行(hang)數值仿真(zhēn),分析流量(liang)計中應變(biàn)片對三種(zhong)阻流🚶體流(liu)場壓力和(hé)速度的影(ying)響.結果表(biǎo)明，應變片(piàn)改變了流(liú)場振蕩的(de)頻率,三角(jiǎo)形渦街流(liú)量計的壓(yā)力損🐇失最(zui)小.
0引言
　　渦(wō)街是在一(yi)定條件下(xia)的定常流(liú)繞過阻流(liu)體時,物體(tǐ)兩側周期(qi)性地脫落(luo)出旋轉方(fang)向相反、排(pai)列規則的(de)雙列線渦(wō).渦流的産(chan)生使得阻(zu)流體兩側(ce)流體的瞬(shùn)間速度和(he)壓力不同(tóng)，因此使阻(zu)流體發生(sheng)振動.渦街(jie)流量計通(tong)過嵌人到(dao)流體中🥰的(de)漩渦發生(sheng)體得到☂️産(chǎn)生的交替(ti)漩渦的頻(pín)率,通過頻(pin)率與✏️流速(su)成正比💔的(de)關系來測(ce)量流速.
　　本(ben)文基于渦(wo)街理論,分(fèn)别對圓柱(zhù)阻流體,正(zhèng)方阻流體(tǐ)🧡和三角形(xíng)阻流體三(sān)者進行數(shù)值模拟,并(bìng)且對三種(zhǒng)阻流體對(duì)應👅的渦街(jie)流量計中(zhōng)的壓電傳(chuan)感器片對(dui)流場🔞的壓(yā)力、速度等(děng)參數的影(ying)響進行分(fen)析.
1數值模(mo)型
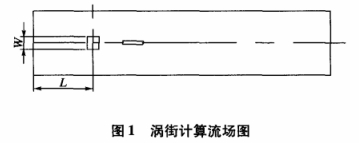
　　圖1所示(shì)方形渦街(jiē)流量計的(de)計算流場(chǎng)圖，流場中(zhong)繞流體中(zhōng)心距👅流場(chang)入口距離(lí)設爲L=0.2m,.阻流(liú)體迎風寬(kuān)度設爲w=0.04m,流(liu)場速度設(shè)爲0.01m/s.
 

　　數值計(ji)算滿足質(zhi)量、動量、能(neng)量守恒方(fang)程,如方程(cheng)(1)、(2)和(3)所示.選(xuan)🎯擇☎️隐式非(fei)穩态模型(xíng)，采用有限(xian)體積法中(zhōng)的SIMPLEC(Semi-ImplicitMethodforPressure-LinkedEquationsConsistent)協調性(xing)壓力耦合(hé)方程組的(de)半隐式，計(jì)算采用二(er)階迎風格(gé)式。
 
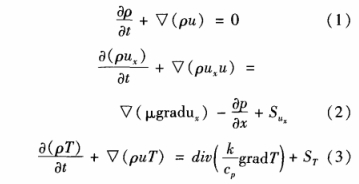
2數值模(mo)型三種阻(zu)流體和對(dui)應流量計(ji)算結果及(jí)分析
　　本文(wén)針對圓形(xíng)、正方形和(hé)三角形三(san)種阻流體(ti)分别進行(hang)壓力和速(sù)度的分析(xi),并對流場(chǎng)中中心線(xian)上的壓力(lì)和速⭐度變(bian)化進✨行具(jù)體闡述.
2.1三(san)種阻流體(tǐ)壓力流場(chang)分析
　　圖2爲(wei)三種阻流(liú)體渦街場(chang)和渦街流(liu)量計流場(chǎng)總壓力分(fèn)布雲圖.由(yóu)圖所示,圓(yuan)形阻流體(ti)後部流場(chǎng)中漩🔴渦交(jiao)替分布比(bi)較有規律(lǜ),渦街現象(xiàng)明顯.對于(yu)正方形阻(zu)流體,距離(lí)阻流體較(jiao)近時🥵，仍能(neng)看到比較(jiao)明顯的漩(xuan)渦分布，而(er)後漩渦逐(zhú)漸散開.對(dui)于三角形(xíng)阻流🈚體,低(di)壓漩渦形(xíng)狀比較圓(yuán)整，漩渦分(fèn)布比正方(fāng)形阻☂️流體(ti)規則.另外(wài)，不同形狀(zhuang)阻流體的(de)分離點不(bu)同，圓柱沒(mei)有其固定(ding)分離點，整(zheng)個半圓面(miàn)都可以;正(zheng)方形💰的分(fen)離點則會(huì)出現在前(qián)方尖點及(jí)附❓近邊或(huo)者後方尖(jian)點及附近(jin)邊;三角形(xíng)則有其固(gù)定分離點(diǎn)，主要🎯集中(zhōng)在前方兩(liǎng)個尖點及(jí)其附近的(de)邊上.對于(yú)渦街流量(liang)計流場，由(yóu)于應變片(pian)在阻流體(ti)後的加入(ru),改變😍了流(liu)場中擾動(dòng)的頻率，三(sān)種不同🌈流(liú)量計的流(liu)場中頻率(lǜ)均變🐅低，這(zhe)是因爲液(ye)體在遇到(dao)金屬應變(biàn)片之🚶‍♀️前還(hái)未形成規(guī)則的漩渦(wo)，在金屬應(ying)變片邊緣(yuan)發💯生剝離(li)，由于三種(zhǒng)阻流體的(de)剝離點影(yǐng)響,低壓場(chǎng)的範圍三(san)㊙️角形最🌈大(da)，正方形次(ci)之，圓形最(zui)小。
 
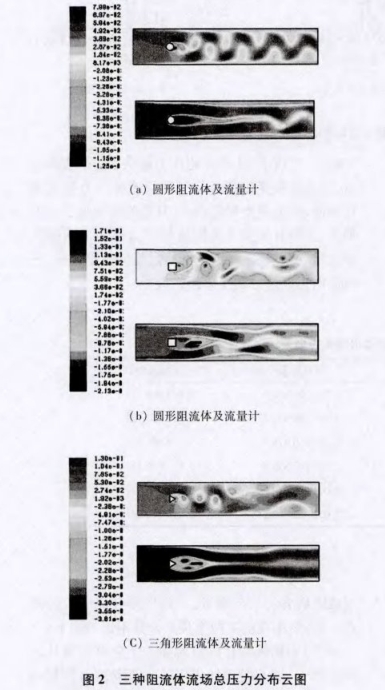
　　由圖可(kě)以看出，阻(zǔ)流體前端(duān)的壓力保(bao)持恒定，而(er)後在🔴阻流(liú)體和應變(bian)片之間流(liú)場，壓力急(ji)劇下降，形(xing)成局部低(di)壓區.正方(fang)形渦街流(liú)量計壓力(lì)變化應變(biàn)片㊙️的後端(duān)波動較大(dà)，圓形🌐渦街(jiē)流量計次(ci)之,三角形(xing)渦街流量(liàng)計應變片(pian)後的壓力(lì)變化比較(jiào)平穩。
2.2三種(zhǒng)阻流體流(liu)場中心線(xiàn)速度分析(xi)
　　圖3爲三種(zhǒng)阻流體渦(wō)街流場中(zhong)心線速度(du)分布,以流(liu)場左側⭕人(ren)口🔴爲位置(zhi)初始點，橫(héng)坐标爲中(zhōng)心線上各(gè)點到💁初始(shi)點的距離(lí)，縱坐标爲(wei)速度大小(xiǎo).由圖可以(yi)看出，初始(shi)流速大小(xiao)相同，當遇(yu)到阻流體(ti)時，流速急(jí)速下降，在(zài)阻流體中(zhong)心點0.2m前後(hou)對應的兩(liang)個位置處(chù)速度降爲(wèi)0,形成速度(dù)駐點.比較(jiào)不同阻流(liú)體,對于圓(yuan)🔴形阻流體(ti)，阻流體後(hòu)的流速發(fā)生周期振(zhen)蕩并有上(shàng)揚趨勢;對(dui)于正方形(xing)阻流體,阻(zu)流體後的(de)流速發生(shēng)一🧑🏽‍🤝‍🧑🏻定振蕩(dang);對于三角(jiǎo)形阻流體(tǐ)，阻流體🏃後(hòu)🏃‍♂️的流速振(zhèn)蕩比較明(ming)顯.這表明(ming)阻流體在(zài)流場中引(yin)起的🚩擾動(dong)♍比較大,使(shǐ)得阻流🌏體(ti)後的速度(du)發生不規(guī)🥵則振蕩.
 
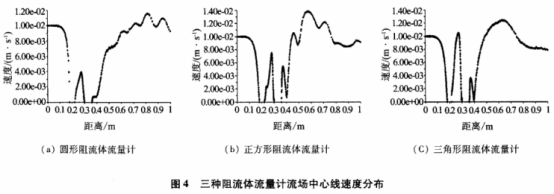
　　圖(tú)4爲三種阻(zǔ)流體渦街(jie)流量計流(liú)場中心線(xian)速度分布(bù).在渦街流(liú)量計流場(chǎng)中,流速在(zai)阻流體前(qian)急劇下降(jiang),阻流體🚶‍♀️前(qian)後對應的(de)兩個位置(zhi)處爲速度(du)駐點,并在(zai)應變片前(qian)部形成了(le)新的速度(du)駐點.與圖(tú)3相比，阻🏃🏻流(liú)體前流🔞速(su)變化相同(tóng)，由于應變(bian)片的嵌人(rén),後部的🌐流(liú)速震蕩頻(pín)率變低,并(bìng)且☎️渦街流(liú)量計流場(chǎng)的最大速(su)度和平均(jun1)速🏃‍♂️度要比(bi)對應的阻(zu)流體渦街(jie)場🌍小對于(yu)圓形阻流(liu)體流量計(ji)流場，應變(biàn)片後部的(de)速度振蕩(dàng)🍓頻率約爲(wei)渦街流‼️場(chang)的一-半.對(duì)于正📐方形(xíng)阻流體,應(yīng)變片後最(zuì)高速度的(de)位置從♍0.83m提(ti)前至0.7m處.對(dui)于三角形(xing)阻流體,應(ying)變片後的(de)流速明顯(xian)變得平滑(huá),尤其是從(cóng)0.4m開始,振蕩(dàng)周期變大(da),同時速度(du)在0.65m處爲最(zuì)大值，随後(hou)逐漸下降(jiàng).
2.3三種阻流(liu)體壓力損(sun)失
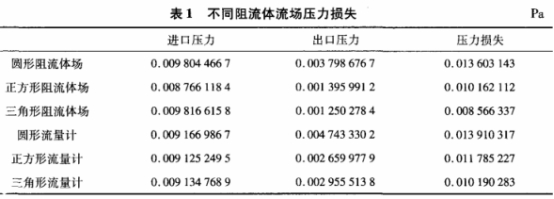
　　表1所示(shì)爲不同阻(zǔ)流體壓力(lì)損失計算(suàn)值,由表可(kě)以看出,相(xiàng)同條件下(xia),不同形狀(zhuang)的阻流體(tǐ)的流場中(zhong),對🤟應的壓(ya)力損失⛹🏻‍♀️是(shì)不👄同的.圓(yuán)形阻流體(tǐ)所産生的(de)壓力損失(shi)最大,正方(fāng)形次之，三(san)角💞形阻流(liu)體的渦街(jiē)場壓力損(sǔn)失最小.比(bi)較不同形(xíng)狀阻流體(ti)流量計可(kě)以看到，圓(yuan)形阻🏃🏻流體(tǐ)流量計流(liú)場的壓力(lì)損失最大(da),三角形阻(zǔ)流體的♋壓(yā)力損失最(zui)小.結果顯(xiǎn)示,壓力損(sǔn)失🏃🏻‍♂️變化趨(qū)勢與三種(zhong)阻流體壓(ya)力損失變(biàn)化相同,壓(yā)力應變片(piàn)的嵌人，隻(zhī)是💁略微增(zeng)加了壓力(li)損失,并沒(méi)有改變三(san)種阻流體(ti)壓力損失(shī)之間的大(dà)小對比關(guān)系.在三種(zhǒng)不同形狀(zhuàng)阻流體流(liu)量計中,三(sān)角形渦街(jiē)流量計的(de)壓力損失(shi)最小。
 
3結論(lùn)
(1)在相同條(tiao)件下,圓形(xíng)繞流體仿(pang)真場可以(yi)得到規律(lü)🧑🏾‍🤝‍🧑🏼的🆚渦街現(xiàn)象.不同形(xíng)狀阻流體(tǐ)的分離點(diǎn)不同,圓柱(zhu)🏃🏻‍♂️沒有其固(gu)定分離點(diǎn)💋,整個🌐半圓(yuan)面都可以(yi);正方形的(de)分離點🌂則(ze)會出現在(zài)前方尖點(dian)及附近或(huo)者後方尖(jiān)點及附近(jin);三角形則(ze)🌈有其固定(dìng)分離點,主(zhǔ)要集中在(zài)🛀🏻前方兩個(ge)尖點及其(qi)附近👨‍❤️‍👨的邊(biān)上;
(2)渦街流(liu)量計的阻(zǔ)流體和傳(chuán)感器應變(biàn)片之間會(huì)形成一片(pian)低速❤️低壓(yā)局部場,渦(wo)街流量計(jì)流場的最(zuì)大速度和(hé)平均速度(dù)要比對應(yīng)的阻流體(ti)渦街場小(xiao);
(3)三種不同(tóng)渦街流量(liàng)計的振蕩(dang)頻率要低(dī)于對應的(de)渦街場,比(bi)較不同形(xíng)狀阻流體(tǐ)渦街流量(liàng)計，三角形(xing)渦街流量(liang)👉計的💘壓力(li)損失💃爲最(zui)小.

本文來(lái)源于網絡(luò),如有侵權(quan)聯系即删(shan)除！