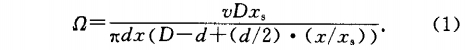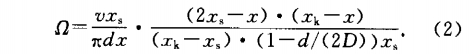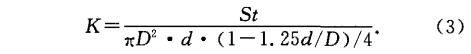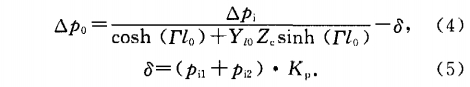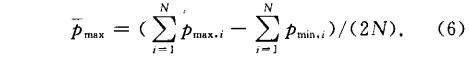摘要:爲了(le)提高渦街流量(liàng)計 的抗幹擾性(xing)和穩定性并保(bao)證測量精度,提(tí)出了一種基于(yú)管壁差壓的旋(xuán)渦頻率檢測新(xīn)方法.在水和空(kong)氣不同管内流(liú)動介質的情況(kuang)下進行了系統(tong)實驗.應用旋渦(wō)動力學和流體(ti)阻抗法,分析了(le)取壓位置和引(yǐn)壓管頻率特性(xing)因素對該方法(fa)測量性能的影(ying)響.結果表明,在(zai)旋渦發生體下(xia)遊的一定距離(lí)内,取壓位置對(dui)該方法的斯特(tè)勞哈爾數和儀(yí)表系數的影響(xiǎng)很小，較靠近旋(xuan)渦發生體迎流(liu)面的地方可測(ce)流量下限低.引(yǐn)壓管的長度應(ying)盡量短,并且保(bǎo)證其固有頻率(lü)與渦街頻率相(xiàng)差較大該方法(fa)簡便可靠,适應(ying)性強,測量下限(xiàn)低.
　　旋渦頻率的(de)檢測是渦街流(liu)量計的關鍵,壓(ya)電晶體法是目(mu)前最爲常用的(de)檢測方法.但是(shi)壓電晶體檢測(cè)法存在兩個嚴(yan)重的問題:1)壓電(dian)晶體對管道的(de)振動較敏感.2)壓(ya)電晶體長期使(shi)用的穩定性差(chà).爲了解決上述(shu)問題,研究人員(yuán)從傳感器的結(jié)構形式和流量(liang)信号的分析處(chu)理等方面進行(háng)了廣泛深人的(de)研究,取得了大(da)量的成果,但是(shì)都難以從根本(běn)上予以解決.
　　 根(gēn)據流體力學基(jī)本原理,在對渦(wō)街流量計流場(chǎng)數值仿真的基(jī)礎上提出了渦(wō)街流量計旋渦(wo)頻率檢測的管(guǎn)壁差壓法,并對(duì)在不同管徑方(fāng)向的取壓位置(zhì)也作了研究.結(jié)果表明,該方法(fa)簡便可靠,不幹(gàn)擾管道内的流(liú)動,抗幹擾性強(qiáng),從而形成一種(zhong)新型.的渦街流(liu)量計,即管壁差(cha)壓式渦街流量(liang)計本文在已有(you)的研究基礎上(shàng),應用旋渦動力(li)學和流體阻抗(kang)法的有關原理(lǐ),從取壓位置和(he)差壓檢測系統(tǒng)兩個方面人手(shǒu),分析了各種因(yīn)素對管璧差壓(ya)式渦街流量計(jì)測量的影響,提(ti)出了相應的解(jie)決方案,爲優化(hua)測量提供了指(zhǐ)導.
1測量原理與(yu)特點
　　 在渦街流(liu)量計中,有旋渦(wo)産生的地方必(bì)有壓力的變化(hua),交替産生的旋(xuán)渦必然會導緻(zhì)附近流場的壓(ya)力出現規則的(de)變化,其變化的(de)頻率與旋渦的(de)頻率一一對應(yīng),因此可以通過(guò)檢測發生體尾(wei)流中某确定的(de)兩點間的波動(dong)差壓來測量旋(xuan)渦頻率,從而實(shi)現流量的測量(liang).由于發生體兩(liǎng)側對稱點上的(de)相位差爲180°,且振(zhen)動幅度和頻率(lü)相等,因此将差(chà)壓取壓位置選(xuǎn)取在管壁上的(de)對稱點更利于(yu)檢測,如圖1所示(shì),其中圖1(a)、(b)分别爲(wèi)沿着管道軸向(xiàng)和徑向的截面(mian)圖.
　　 數值仿真結(jie)果都表明,與目(mù)前常用旋渦頻(pin)率檢測方法相(xiàng)比,管壁差壓法(fa)具有以下明顯(xiǎn)優勢:1)引壓系統(tǒng)對管内待測介(jiè)質流動幾乎沒(méi)有影響;2)傳感器(qì)系統獨立于旋(xuan)渦發生體,并且(qie)位于管道外面(miàn)，維修和更換時(shí)不需要切斷管(guǎn)流拆卸旋渦發(fā)生體,可以實現(xiàn)傳感器在線維(wei)修和更換;3)與壓(ya)電晶體法相比(bǐ)，具有較強的抗(kàng)幹擾性;4)可測流(liú)量下限低.
 
2過程(cheng)與裝置
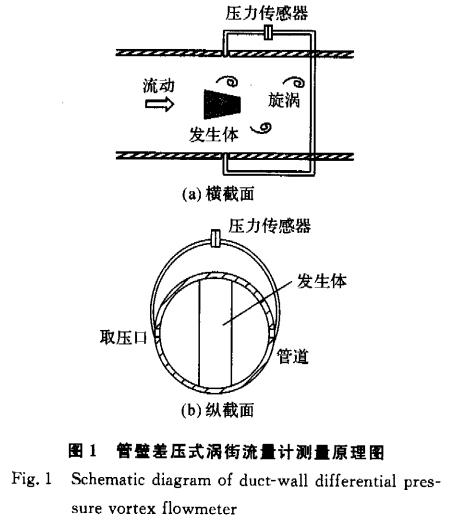
　　 在管内(nèi)流動介質分别(bie)爲水和空氣的(de)情況下均進行(háng)了實驗,整個測(cè)試由動力設備(bèi)、穩壓設備、标準(zhun)流量表、前直管(guan)段、實驗段和後(hou)直管段6部分組(zu)成.管道的内直(zhí)徑D=50mm,旋渦發生體(tǐ)的橫截面爲梯(tī)形,迎流面寬度(dù)d=14mm,管壁差壓的取(qu)壓孔選擇在發(fa)生體後的三對(dui)不同位置1、2、3,它們(men)分别位于距發(fā)生體迎流面0.2D、0.5D、D的(de)下遊，其中D爲管(guan)道内直徑,如圖(tú)2所示.
　　 空氣和水(shui)的标準流量表(biao)分别爲鍾罩标(biao)準流量裝置和(he)電磁流量計,它(ta)們的精度均爲(wèi)0.5級.測得的管壁(bì)差壓經過放大(da),由數字示波器(qi)記錄保存,再導(dǎo)人計算機進行(háng)處理分析.
 
3取壓(yā)位置的影響
3.1渦(wō)街流計内的旋(xuán)渦特性
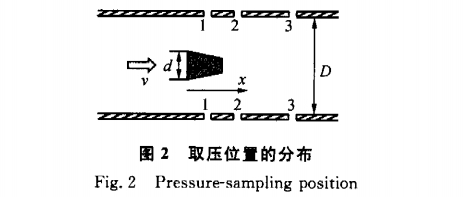
　　 由于管(guǎn)壁的約束,渦街(jie)流量計中旋渦(wō)的産生和脫落(luo)特性并不和自(zi)由流場中的情(qing)況完全相同.渦(wō)街流量計中旋(xuán)渦發生體下遊(yóu)的旋渦區可以(yǐ)分爲3個區段，即(ji)密集發展段、穩(wěn)定段和旋渦消(xiāo)散段.在密集發(fa)展段,旋渦旋度(du)2(即渦量)沿流動(dòng)方向x的變化規(gui)律爲.
 
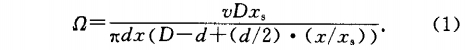
　　式中:v爲管(guǎn)内平均流速,D爲(wei)管道内直徑,d爲(wei)旋渦發生體迎(yíng)流面寬度,xs爲密(mi)集發展段的長(zhǎng)度.
　　 在穩定段,旋(xuan)渦旋度爲
 
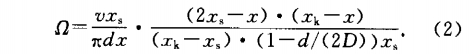
　　式中(zhong):xk爲密集發展段(duàn)和穩定段的總(zǒng)長度.
　　由于d、D、x,和xk均(jun1)爲常數,根據式(shi)(1),(2)可見,不論是在(zai)密集發展段還(hai)是在穩定段,旋(xuan)渦旋度Ω都是正(zheng)比于流速v,且随(sui)x的增大而減小(xiao).
　　在旋渦消散段(duan),由于流層之間(jian)的相互作用能(néng)量逐漸消耗,旋(xuan)渦逐漸消失.
3.2不(bu)同取壓位置的(de)實驗結果與比(bi)較
3.2.1斯特勞哈爾(ěr)數和儀表系數(shu)渦街流量計
　　用(yong)于測量的前提(tí)條件是在--定的(de)雷諾數Re範圍内(nei)儀.表系數K保持(chí)爲常數,對于渦(wō)街流量計,由于(yu)K與斯特勞哈爾(ěr)數St存在如下關(guan)系:
 
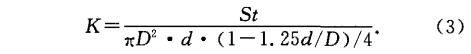
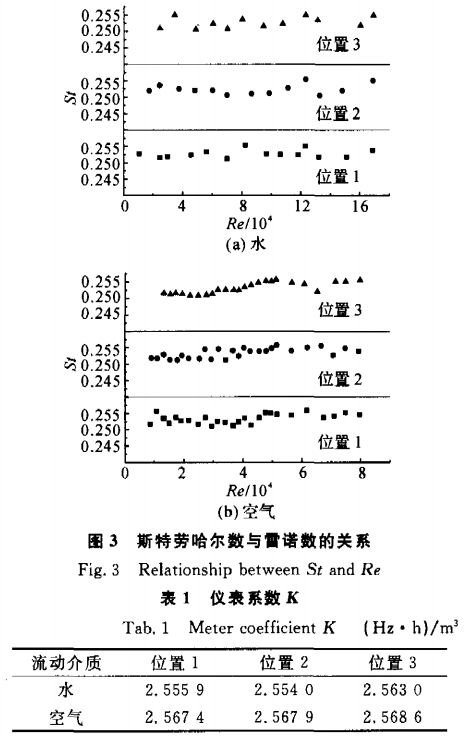
　　因此要求在(zai)一定的雷諾數(shu)Re範圍内St保持不(bu)變.不同流動介(jie)質、不同取壓位(wei)置的St與Re的對應(yīng)關系如圖3(a)、(b)所示(shi).各種情況的St基(ji)本上保持爲常(chang)數,且它們的值(zhí)均相等,約爲0.253.各(gè)種情況的儀表(biao)系數列于表1,它(ta)們之間的最大(dà)相對誤差小于(yú)1%,這表明在旋渦(wo)發生體後一定(ding)的距離内，流動(dòng)介質和取壓位(wèi)置對管壁差壓(yā)式渦街流量計(ji)的測量影響很(hěn)小.
 
3.2.2最小可測流(liu)速
　　渦街流量計(jì)測量下限的拓(tuò)展一直是研究(jiu)的熱點.各種情(qíng)況的最小可測(ce)流速及常規渦(wo)街流量計的測(ce)量下限列于表(biǎo)2.在實驗中,越靠(kào)近發生體,旋渦(wō)的旋度強，測量(liàng)的靈敏度高，不(bu)論是水還是空(kōng)氣,最小可測流(liú)量都是随取壓(ya)位置的後移而(ér)增大.當測量水(shuǐ)時,位置1的測量(liàng)下限僅爲常規(gui)表的52%;當測量空(kong)氣時,位置1的測(cè)量下限爲常規(gui)表的75%,因此采用(yòng)管壁差壓法能(neng)有效地降低渦(wō)街流量計的測(cè)量下限,将取壓(ya)位置适當靠近(jin)發生體能進一(yī)步降低測量下(xia)限.
 
引壓管的影(ying)響
4.1引壓管動态(tai)特性的數學模(mo)型
　　根據流體阻(zu)抗法的集中參(cān)數模型,若差壓(ya)傳感器兩根引(yin)壓管的平均長(zhǎng)度爲Ɩ0,平均導納(nà)爲YƖ0,輸入的管壁(bì)正弦脈動壓力(li)差△pi=pil-pi2,則傳至差壓(yā)傳感器的差壓(yā)爲
 
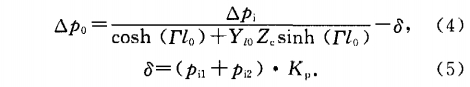
　　式中:F=√ZY爲引壓(yā)管單位長度的(de)傳播常數;Z和Y分(fen)别爲單位長度(du)的串聯阻抗和(hé)并聯導納;Zc=√Z/Y爲管(guan)路的特性阻抗(kang);δ爲差壓測量的(de)絕對誤差;K。爲壓(yā)力脈動影響系(xi)數.
　　在兩段引壓(yā)管長度較短且(qie)相差不大,差壓(ya)傳感器壓力腔(qiāng)室很小的條件(jiàn)下,當輸人差壓(ya)脈動頻率ƒ低于(yú)引壓管的基本(běn)頻率ƒ。的1/2時，Kp<0.03,δ值較(jiào)小;當ƒ>0.5ƒ。時,Kp随ƒ的增(zēng).加而顯著上升(shēng),δ值較大.
4.2管壁差(chà)壓平均幅值的(de)測最偏差與讨(tao)論
管壁差壓平(ping)均幅值`Pmax定義爲(wèi)
 
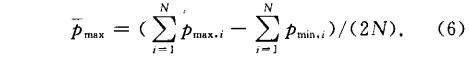
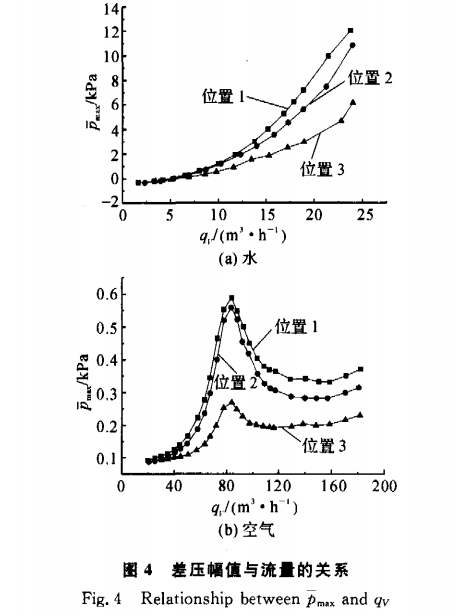
　　式中:Pmax.pmin,;分别爲第(di)i個旋渦周期内(nei)管壁差壓的最(zui)大值和最小值(zhí);N爲檢測的總周(zhou)期數. `Pmx值反映了(le)旋渦強度的大(dà)小,應随流量的(de)增加而增大.實(shí)驗`Pmx與qv的關系如(ru)圖4所示,當圖4(a)中(zhong)給出的是流動(dong)介質爲水時,從(cong)3對不同取壓位(wei)置測量的`Pmx随qv的(de)分布情況,可見(jian)3條曲線均随qv的(de)增加而單調遞(di)增,較好地符合(he)了理論預測;圖(tu)4(b)中所示的是流(liu)動介質爲空氣(qi)時的情況,3條曲(qu)線的形狀相似(sì),當qv<83m3/h,`Pmx随流量的增(zēng)加而增大,在qv=83m3/h附(fu)近取得極大值(zhi),當qv>83m3/h,`Pmx不再随流量(liàng)的增加而增大(dà),而是急劇下降(jiàng)直至qv>120m3/h後逐漸平(píng)緩遞增.
　　當流量(liàng)qv=83m3/h時，旋渦頻率ƒ=213Hz,K=2.5680Hz·h/m;引(yǐn)壓管的長度Ɩ=0.20m,其(qí)固有頻率ƒ0=c/(4Ɩ)=425Hz,c爲引(yǐn)壓管中介質的(de)聲速，則ƒ=0.5ƒ0..當qv>83m3/h,ƒ>0.5ƒ0,Kp随ƒ的(de)增加而顯著上(shang)升,差壓測量的(de)絕對誤差δ值增(zēng)大.因此較低的(de)引壓管固有頻(pin)率阻礙了測壓(yā)系統對動态管(guǎn)壁差壓的響應(yīng),從而造成較大(dà)的測量誤差,與(yu)理論關系不符(fú).爲了克服或減(jiǎn)小引壓管對測(ce)量的影響,應盡(jin)量縮短引壓管(guǎn)的長.度.但是管(guan)壁差壓幅值的(de)誤差并沒有影(ying)響頻率的測量(liàng),對St和K的影響甚(shen)小,也即流量的(de)測量幾乎不會(hui)受影響,說明管(guan)壁差壓法的強(qiang)适應性和穩定(dìng)性.
 
5結論
(1)在發生(sheng)體下遊的一定(dìng)距離内,取壓位(wèi)置對管壁差壓(yā)式渦街流量計(jì)的斯特勞哈爾(ěr)數和儀表系數(shù)的影響很小;
(2)管(guǎn)壁差壓式渦街(jiē)流量計的測量(liang)下限随取壓位(wèi)置的不同而顯(xiǎn)著變化，在旋渦(wō)發生體後的一(yī)定範圍内,較靠(kao)近發生體迎流(liú)面的地方測得(de)的最小流速低(dī)于遠離迎流面(mian)的地方;
(3)引壓管(guǎn)的響應頻率對(dui)管壁差壓式渦(wo)街流量計的測(cè)量有着重要的(de)影響,爲了保證(zhèng)準确測量,應盡(jin)量縮短引壓管(guan)的長度,并且保(bao)證引壓管固有(yǒu)頻率與渦街頻(pín)率相差較大.
　　由(you)于工業現場的(de)流動狀态複雜(za),因此進一步工(gōng)作将圍繞着該(gai)方法在旋轉流(liu)、脈動流等惡劣(lie)工況下的性能(néng)展開.

本文來源(yuan)于網絡,如有侵(qīn)權聯系即删除(chú)！