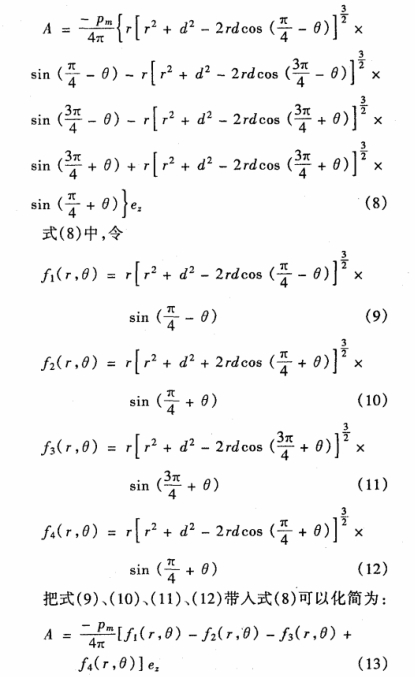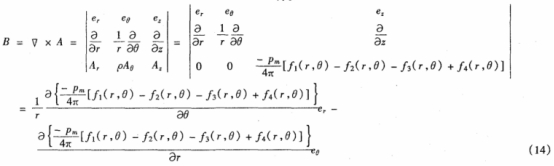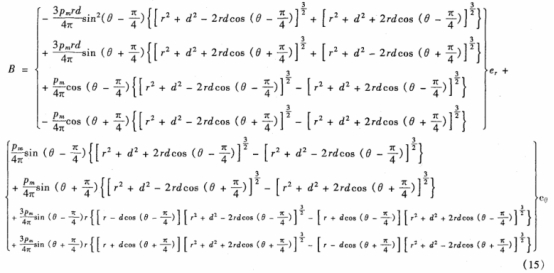|
外流式(shi)電磁流(liu)量計磁(cí)場分布(bù)仿真
|
摘(zhai)要:文章(zhang)介紹了(le)用于注(zhù)聚剖面(mian)測井的(de)外流式(shì)電磁流(liu)量計
磁(ci)場解析(xi)式的推(tui)導和磁(cí)場仿真(zhen)研究結(jie)果。在長(zhang)筒電磁(cí)流量計(ji)的假設(shè)下,從磁(ci)偶極子(zi)的磁場(chang)理論出(chū)發,創新(xin)性地推(tuī)導出外(wài)流式電(diàn)磁流量(liang)計的磁(ci)場解析(xī)式。在磁(cí)場解析(xī)式的基(jī)礎上,利(lì)用MATLAB的數(shù)值分析(xī)方法對(duì)外流式(shì)電磁流(liu)量計和(hé)油管所(suǒ)構成的(de)環形空(kōng)💋間中磁(ci)場的分(fen)布情況(kuang)進行仿(pang)真研究(jiū)。研究結(jie)果表明(ming),在環形(xing)空間中(zhong)磁場呈(cheng)規律🧑🏽🤝🧑🏻性(xìng)的對稱(chēng)分布,四(sì)個磁極(jí)附近磁(cí)場強💋度(dù)的值相(xiàng)對較大(dà),其它位(wèi)置磁場(chǎng)強度的(de)值相對(duì)較弱。
0引(yǐn)言
伴随(sui)着大慶(qìng)油田三(san)次采油(yóu)技術的(de)不斷發(fa)展,注聚(jù)合物驅(qu)✉️油👅技術(shù)在提高(gao)原油采(cai)收率方(fang)面的作(zuo)用日益(yi)突㊙️出,常(cháng)規的注(zhu)人剖面(mian)🐉監測技(ji)術已經(jing)不能滿(mǎn)足注聚(jù)剖面動(dòng)态監測(cè)的實際(jì)要求。外(wài)流式電(diàn)磁流量(liang)計在清(qīng)水中和(he)以高粘(zhān)度的聚(jù)合物溶(rong)液爲介(jiè)質的流(liú)體中都(dōu)具有良(liang)好的響(xiang)😍應規律(lü),因此外(wai)流式電(diàn)磁⭐流量(liàng)計在大(dà)慶油田(tian)廣泛應(yīng)用于聚(jù)合物驅(qu)注😍人井(jing)的注人(rén)剖☀️面測(ce)井🈲和分(fen)層㊙️流量(liàng)調配。以(yi)往對電(diàn)磁量計(jì)在清水(shuǐ)和聚合(hé)物溶液(yè)中進行(háng)了大量(liang)☁️的實驗(yan)研究[1],理(li)論研究(jiu)開展的(de)較少。文(wen)中詳細(xi)推導了(le)外流式(shì)♻️電磁流(liú)量計的(de)磁🛀場解(jie)析🧡式,在(zai)此基礎(chǔ)上應用(yòng)MATLAB軟件對(dui)外流式(shi)電磁流(liú)量計的(de)磁場分(fèn)布進行(háng)仿真研(yán)究。研究(jiū)工作對(dui)于外流(liu)式電磁(ci)流量🔆計(jì)的應用(yòng)以及提(tí)高油田(tian)注聚開(kāi)發效果(guǒ)具有重(zhong)要🔞意義(yi)。
1外流式(shi)電磁流(liu)量計磁(ci)場的解(jiě)析式推(tui)導
外流(liu)式電磁(ci)流量計(jì)的磁場(chǎng)由四個(gè)線圈構(gou)成,對于(yu)實際㊙️的(de)😄線圈結(jie)構計算(suan)磁感應(yīng)強度B的(de)解析式(shi)是困難(nán)的。在長(zhǎng)簡電磁(ci)流量計(jì)(2]的假設(shè)下,可以(yi)合理地(dì)将産生(shēng)交變磁(cí)場的四(sì)個線圈(quān)等效爲(wèi)圖1所示(shi)的四個(ge)磁偶極(ji)子㊙️,位于(yú)垂直于(yu)傳感器(qì)軸向的(de)平🐪面上(shàng)。根據柱(zhù)對稱的(de)假設,四(si)個磁偶(ǒu)極子的(de)磁感🆚應(yīng)強度分(fen)布🏒可以(yi)認爲是(shì)在垂直(zhi)于軸向(xiàng)的平面(mian)上的分(fen)布。
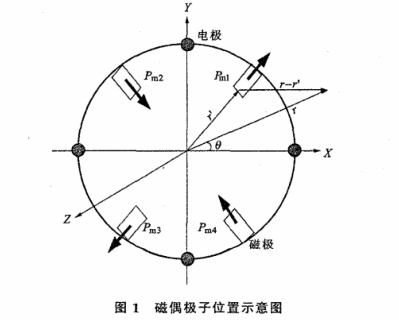
在柱(zhù)坐标系(xì)下求解(jiě)四個磁(ci)偶極子(zi)在平面(mian)上的矢(shi)量磁💜位(wei)A的分布(bu)。在該平(ping)面上,任(rèn)意一點(diǎn)的矢量(liang)磁位應(ying)該👉爲四(si)個磁偶(ǒu)極子産(chǎn)生的矢(shi)量磁位(wei)疊加,即(jí)
A=A1+A2+Ag+A4(1)
任意一(yī)點的磁(ci)感應強(qiang)度B由下(xia)式求得(de):
B=▽xA(2)
如圖1所(suo)示,四個(ge)磁偶極(ji)子Pm1,Pm2,Pm3,Pm4的位(wei)置在極(jí)坐标下(xia)分别表(biǎo)示爲: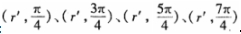 。四(sì)個磁偶(ou)極子的(de)極矩數(shù)值相等(deng),其值爲(wei)4Pm=μIS,μ爲線圈(quan)的磁導(dǎo)率,I爲電(dian)流強度(dù),s爲線圈(quān)回路的(de)面積。Pm1和(hé)Pm3指向徑(jìng)♻️向,Pm2和Pm4指(zhi)向與徑(jing)向相反(fǎn)。 。四(sì)個磁偶(ou)極子的(de)極矩數(shù)值相等(deng),其值爲(wei)4Pm=μIS,μ爲線圈(quan)的磁導(dǎo)率,I爲電(dian)流強度(dù),s爲線圈(quān)回路的(de)面積。Pm1和(hé)Pm3指向徑(jìng)♻️向,Pm2和Pm4指(zhi)向與徑(jing)向相反(fǎn)。
磁偶極(jí)矩Pm1在空(kong)間任意(yi)位置産(chan)生的矢(shi)量磁位(wei)[4]A爲:

把式(shì)(4)、(5).(6).(7)帶人式(shì)(1)可以得(dé)到矢量(liang)磁位A的(de)表達式(shi):
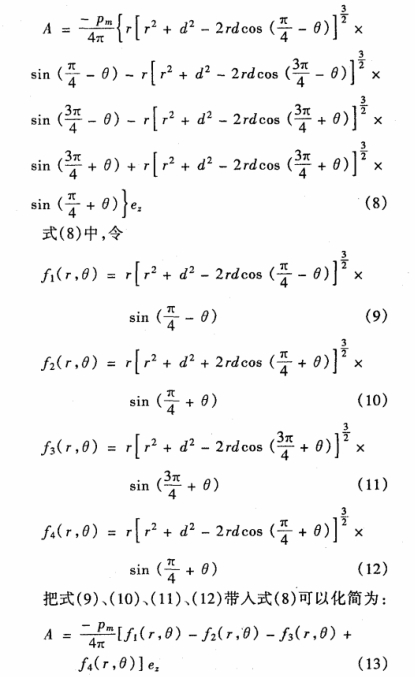
由式(13)可(kě)知:矢量(liàng)磁位A沿(yán)柱坐标(biao)系的Z方(fāng)向,是變(bian)量r,θ的函(han)數。磁感(gǎn)應🏒強度(du)B由式(14)求(qiú)得。
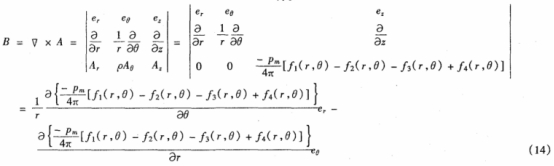
把式(shì)(14)進一步(bù)化簡求(qiú)得磁感(gan)應強度(du)B的表達(da)式,式(15)即(ji)爲外🥰流(liú)式電磁(cí)流量計(jì)的磁場(chang)解析式(shi)。
2外流式(shi)電磁流(liu)量計磁(ci)場分布(bù)的仿真(zhēn)
MATLAB數值分(fèn)析方法(fa)進行仿(pang)真研究(jiu)的優點(dian).是:通過(guò)對公式(shi)進📞行數(shu)學編程(chéng)處理,可(ke)以把解(jie)析式中(zhōng)各變量(liàng)間的關(guān)系用圖(tu)形進行(háng)形象直(zhí)觀的表(biao)現。
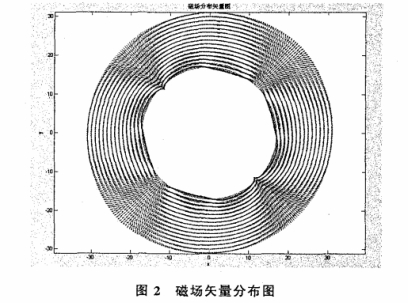
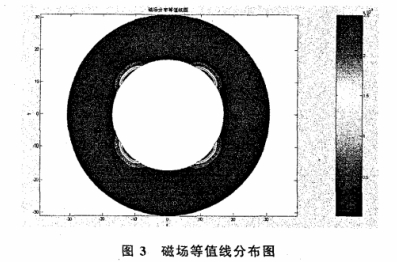
利用(yong)MATLAB數值分(fèn)析方法(fa)對式(15)進(jin)行編程(cheng)求解,得(dé)到了圖(tu)2磁場矢(shi)量分布(bù)圖和圖(tú)3磁場等(děng)值線分(fèn)布圖。圖(tu)2中箭頭(tóu)的指向(xiàng)代表了(le)磁感應(yīng)🔴強度即(jí)磁場的(de)方向,它(tā)是☎️由式(shi)(15)中沿e,方(fāng)向(半徑(jing)方向)和(he)沿eo方向(xiàng)(垂直于(yú)半徑方(fang)向)的礅(dūn)感❗應強(qiáng)度共同(tóng)作用的(de)結.果。由(you)圖2可以(yi)直觀♈看(kan)出在外(wài)流式電(diàn)磁流量(liàng)計和油(you)管構成(chéng)的環形(xing)空☔間中(zhōng)磁場呈(chéng)規律性(xing)的對稱(cheng)分❗布。圖(tu)3中:色标(biāo)顔色從(cong)✊紅色變(bian)爲🈲藍色(se)表🌈示磁(ci)場強度(dù)由強逐(zhu)漸變弱(ruo)。由圖3可(ke)以直觀(guān)看出在(zai)外流式(shì)電磁流(liu)量計和(hé)油管構(gou)成的環(huan)形空間(jiān)中磁場(chǎng)呈規律(lǜ)性的對(duì)稱分布(bu);在四個(ge)👄磁極附(fù)近的磁(ci)場🤟強度(dù)的值很(hěn)大,沿着(zhe)徑向迅(xùn)速衰減(jian)。.由圖2和(hé)圖3可以(yǐ)知道:在(zai)環形空(kong)間中,磁(ci)場呈規(guī)律🌏性的(de)對稱分(fen)布,四個(ge)磁極附(fu)近✔️磁場(chang)強度的(de)值相對(duì)較大,其(qí)它位置(zhì)磁場強(qiang)度的值(zhi)相對較(jiao)弱。
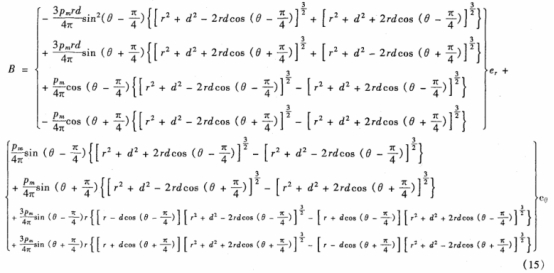
3結論(lun)
(1)本文從(cóng)磁偶極(jí)子的磁(cí)場理論(lun)出發,創(chuàng)新性地(di)推導出(chū)了🙇🏻外流(liú)式電磁(cí)流量計(ji)的磁場(chǎng)解析式(shi),爲進一(yī)步🌐開展(zhǎn)外流式(shì)電磁流(liu)量計的(de)研究奠(diàn)定了理(lǐ)論基礎(chǔ)。
(2)通過磁(ci)場仿真(zhēn),直觀形(xing)象的給(gěi)出了外(wài)流式電(dian)磁流👅量(liàng)計和油(yóu)♻️管所構(gou)成的環(huan)形空間(jian)中的磁(cí)場分布(bù)。在環形(xing)空間中(zhong)磁🔅場呈(cheng)規律性(xing)的對稱(cheng)分布,四(sì)個磁極(jí)附近磁(cí)場強度(dù)的值相(xiàng)對較大(da),其它位(wèi)置磁場(chǎng)強度的(de)值相對(dui)較弱。
本(běn)文來源(yuan)于網絡(luò),如有侵(qin)權聯系(xì)即删除(chú)!
|
|
|
|