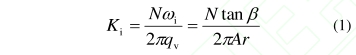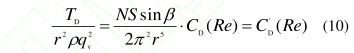摘要(yào):渦輪流量計 的(de)精度受被測介(jiè)質及其運動粘(zhān)度變化的影響(xiang)。使用體積流量(liang)⭕和儀表系數無(wú)法從變粘度實(shi)驗中取得形态(tai)-緻🧑🏽‍🤝‍🧑🏻且可預測的(de)标定結果。應用(yong)量綱分析導出(chū)雷諾數和斯特(te)勞哈爾數作爲(wei)描述渦輪流量(liàng)計✏️性能的無量(liàng)綱參數。通過改(gai)變丙二醇-水溶(rong)液的體積濃度(du)得到五個不同(tong)運動粘度的介(jie)質，分别用于标(biāo)定一台DN25渦輪💜流(liú)量計。對比結果(guǒ)表明，不同粘度(dù)下的标定曲線(xiàn)在雷🐆諾數小于(yu)7400區域出現分離(li)，标定數據最大(dà)相差0.9%。随着雷🌍諾(nuo)數增加，儀表系(xi)數中軸承阻滞(zhi)部分的影響相(xiàng)對減小，标定曲(qǔ)線簇由分散趨(qū)于聚攏，标定數(shu)據差異小于0.1%。葉(yè)片表面的流動(dong)邊界層發生層(ceng)淌轉捩時阻力(lì)的突變導緻标(biao)定曲線出現駝(tuo)峰，運動粘度越(yue)低，駝峰趨于👈平(píng)緩。軸承阻滞中(zhōng)的🧑🏽‍🤝‍🧑🏻靜态阻力✌️部(bu)分是造成相同(tóng)雷諾數下儀表(biao)系數差🧑🏾‍🤝‍🧑🏼異的主(zhu)要原因，這種差(cha)異随雷諾數👈減(jian)小而增加，所🌈以(yi)，當校準介質和(hé)工作介質的運(yùn)動粘度有顯著(zhe)差異時，渦輪流(liú)量計要避免工(gōng)作在低雷諾數(shù)區域 。
0引言
　　渦輪(lun)流量計是一種(zhong)可靠的，用于測(cè)量流體流量的(de)儀表❄️。石油、化工(gong)領域大量使用(yong)渦輪流量計測(ce)量輸運天然氣(qi)、燃料油和烴類(lèi)流體的流量，渦(wō)輪流量計的精(jing)度🏒對于涉及能(néng)源的貿易交接(jie)非常重要。自從(cóng)🌏1790年ReinhardWoltman使用第一台(tái)渦輪流量計測(ce)😄量水流量以來(lái)，渦輪流量計經(jīng)曆🐇了許多變化(huà)和改進，仍然被(bei)認爲是一種準(zhun)确且穩定的工(gong)業儀表",在穩定(dìng)條件下， 液體渦(wō)輪流量計 的精(jīng)度可以達到0.1%， 氣(qi)體渦輪流量計(jì) 的精度可以達(dá)到0.5%121。
　　通常情況下(xia)，計量技術機構(gòu)或校準實驗室(shì)使用某一🤞種流(liu)體(一般是水)校(xiao)準渦輪流量計(jì)，而實際被測對(duì)象🌍常常是另外(wai)-一種介質。即使(shi)校準和工作場(chǎng)合中使用同一(yī)種介質，液體的(de)運動粘度易受(shou)溫度變化影響(xiang)，渦🔞輪流量計性(xing)能會有較大的(de)差異，需要增加(jia)額外的校準工(gōng)作。例如，在油品(pǐn)或烴類介質的(de)貿易交接中，如(ru)🥰果更換了管道(dào)中的介質或介(jie)質的物性發生(shēng)較大變化，都要(yao)對渦輪流量計(ji)進行--次現場重(zhòng)新校準。
　　以往的(de)研究表明，渦輪(lún)流量計在低粘(zhan)度流體(1mm2/s及以下(xià))和高粘度流體(ti)((50~100)mm2/s)下的标定曲線(xiàn)形态有很大不(bú)同4。雖然對此已(yi)有🐉很多研究和(he)報道[5),但粘度影(yǐng)響渦輪流量計(jì)性能的流體動(dòng)力學機🔞理仍未(wèi)被完全理解161。已(yǐ)經發表的渦輪(lun)流量計物理模(mo)型大多基于動(dòng)量和氣翼理論(lùn)💞，但這些模型🚶都(dou)依賴于實驗數(shu)據的修正，還沒(méi)有一個經過廣(guǎng)泛驗證的物理(lǐ)模型能夠充☎️分(fen)解釋渦輪流量(liàng)計的輸出響應(yīng)以及标定曲線(xiàn)的變化細節。
　　近(jin)年來，借助計算(suan)流體力學(computationalfluiddynamics,CFD)模拟(ni)研究了流量計(jì)内部的流🌈場，分(fèn)析影響渦輪機(ji)流量計精度的(de)因素，通過優化(huà)結🌈構參數來提(ti)高流量計的性(xìng)能。提出一種針(zhen)對液體渦輪流(liú)量計葉輪的多(duō)參數🔞定量優化(hua)方法，以減少粘(zhan)度對傳感器特(te)性的影響。根據(ju)CFD軟件計算得到(dao)的流場信息解(jie)釋流體粘度變(biàn)化影響傳感器(qi)性能的機制。在(zài)其提出的數值(zhí)模型中考慮了(le)軸💛承阻力矩，通(tong)過CFD計算預測渦(wo)輪流量計的性(xing)能。通過🏃🏻‍♂️CFD模🔞拟分(fen)析了，上遊整流(liú)件的結構參數(shù)對🏒渦輪流量🔆計(ji)性能的影響，并(bing)提出了整流件(jian)結構的優化方(fāng)案✨。定義了一個(gè)表征葉輪葉片(pian)形狀的結構👌參(can)數，通過🏃🏻‍♂️CFD模拟分(fen)析渦輪流量計(jì)内部流場，解釋(shi)葉片結構對其(qi)性能的影響機(jī)制。
　　上述研究都(dou)是基于轉子系(xì)統的力矩平衡(héng)，通過改變☎️流體(tǐ)物性計算相應(yīng)的流場信息，進(jìn)而得到流量計(ji)的輸出響應。相(xiàng)較而言😄，通過實(shí)驗研究儀表系(xi)數🤞和标定曲線(xiàn)的演化規🛀律，人(rén)們能夠更直觀(guan)地了解儀表對(duì)實💋際工況的響(xiǎng)應。本文基于動(dòng)量方法的基本(ben)表達式，應🔱用量(liang)綱分析導出雷(léi)諾數(Reynoldsnumber,Re)和斯特勞(lao)哈爾數(Strouhalnumber,Sn)作爲描(miao)🏃🏻述🚩渦輪流量計(ji)性能的無量綱(gāng)參數。分别使用(yong)五種運動粘度(dù)((1.02~30)mm2/s)介質标定一台(tái)DN25渦輪流量計，實(shí)驗數據揭示了(le)受粘度變化影(ying)響的儀表系數(shù)在低雷諾數區(qū)域出現明顯差(chà)異，以及由于層(ceng)湍轉捩🤟時阻力(lì)變化所導緻的(de)駝峰形标定曲(qǔ)線💋在粘度影❓響(xiang)下的分布💋規律(lǜ)。
1研究對象及其(qi)出廠标定數據(jù)
　　圖1所示的是一(yī)台8個葉片的DN25渦(wō)輪流量計的轉(zhuan)子結㊙️構。流量計(jì)的量程範圍是(shi)(0.6~12)m/h。爲了使該流量(liàng)計适用于多種(zhong)粘度介質，制造(zào)商在出廠标定(dìng)時使用五種烴(tīng)類介質，标定結(jie)果用體積流量(liang)qv和儀表系數K表(biao)示(如圖2所示)。相(xiàng)💋對于低粘度介(jiè)質，高粘度介質(zhi)((28~-788)mm2/s)下的儀表系數(shu)與體積♍流量呈(chéng)現高度非線性(xing)。标♌定曲線随粘(zhān)度的改變出現(xian)偏移，流量越小(xiǎo)，偏移量越大，以(yi)運動粘度v=1.09mm2/s的儀(yí)表系數爲參考(kǎo)，體積流量qv=1.2m2/h時其(qí)餘四個粘度的(de)儀表系數分别(bie)☁️偏移0.5%、2.6%、14.6%和50.3%，可見qv-K标(biao)定曲線并不适(shi)用，需要重新選(xuan)擇兩個參數分(fèn)别代表來流的(de)㊙️标準值和流量(liang)計的輸出響應(yīng)。爲此，對渦輪流(liú)🌂量計物理模型(xing)的表達式作量(liàng)綱分析。
 
2量綱分(fen)析
　　作爲體積流(liú)量的直接體現(xian)，渦輪流量計的(de)旋轉角速❗度ɷ和(he)通過流量計區(qū)域的流速V成正(zhèng)比。理想情況下(xià)的🌂流量計儀表(biǎo)系數Ki是一個常(cháng)數，由流量計的(de)幾何形狀和尺(chi)寸決定，與實際(ji)流🌈量或流動狀(zhuàng)态無關，即
 
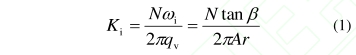
　　式中(zhong),A是流量計葉片(piàn)進口處的流道(dao)截面積，N是葉片(pian)數🏃，qv是體積流量(liàng)，r是葉片邊緣處(chù)的半徑和輪毂(gu)半徑💛的均方根(gēn)，即平均有效半(ban)徑，β是r對應的葉(yè)片角度。實🙇🏻際情(qing)況下，葉片受到(dao)的阻滞力矩T,使(shi)轉子實際旋轉(zhuan)🛀角速度w低于理(li)想角速度ɷi，于是(shì)，實際儀表系數(shu)K.爲:
 
　　量綱分析的(de)第一步是從所(suǒ)研究方程中确(què)定合适的變量(liang)✂️，第👈二步是選擇(ze)π方程的基本變(bian)量，第三步是确(què)定每個π表達🌏式(shì)中✉️基本變量的(de)指數，最終确定(ding)關鍵的無㊙️量綱(gāng)參數。式(3)中🔴有f、qvr、B、ρ和(he)Tr六個變量,.還有(you)一個物性變量(liàng)一動力粘度μ隐(yǐn)含在方♉程中，動(dòng)力粘度影響流(liú)量計流道中的(de)速度剖面分布(bù)，以及流體沿葉(ye)片💋表面和輪毂(gu)的流動阻力，所(suo)以，量綱分析需(xū)要使用🙇🏻七個變(biàn)量。
　　從式(3)中選擇(ze)的第一個變量(liàng)是頻率f,量綱單(dān)位是T';第二個變(biàn)量是流速V,相對(duì)于體積流量q(包(bao)含面積單位),流(liú)速是一個更基(jī)本的變☂️量,量綱(gang)單位是LT;第三個(gè)變量是平均有(yǒu)效半徑r,這裏使(shǐ)用🌈更容易确定(ding)和标準化的流(liú)量♊計直徑D代替(tì)，量綱單位是L;第(di)四個變量是葉(yè)片角度β,這裏使(shǐ)用一個簡單的(de)長度l代替,量綱(gang)單位是L;兩個流(liu)體物性變量密(mi)度p和動力粘度(dù)u,量綱單位分别(bié)是ML-3和是ML-1T-1;最後一(yi)個變量是阻力(lì)矩T,量綱單位是(shì)M.L2T-2。
　　七個選定的變(biàn)量中流速V、流量(liang)計的尺寸D和l決(jue)定了儀表本身(shen)的🔞性能。流體物(wù)性p、μ和阻力矩T;影(ying)響儀表的實際(ji)性能🍉。七個變量(liang)包含三個量綱(gāng)單位(L、M和T)，故選擇(zé)三個變⛱️量(D、V和p)作(zuò)爲基本♋變量。四(sì)個π方程(7個變量(liang)-3個量綱單位=4個(ge)方程)如式🌈(4)所示(shi)。
 
性能，故舍去。進(jin)一步轉化T2得到(dào)關于儀表系數(shù)K的斯特勞✏️哈爾(ěr)數(Strouhalnumber,St)::
 
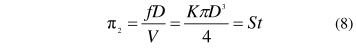
　　将雷諾數作(zuò)爲标定數據的(de)橫坐标，代表标(biao)準流量值，将💜斯(si)🐕特✔️勞哈爾數作(zuò)爲标定數據的(de)縱坐标，代表流(liu)量計對💜于标準(zhǔn)流🏃🏻‍♂️量值♍的輸出(chū)響應。渦輪流量(liàng)計🔞出廠标定數(shù)據的Re-St散點如圖(tú)3所🔆示，流量計在(zai)不同粘度介質(zhì)下的輸出響應(yīng)被重整🤞爲一條(tiao)和雷諾數有關(guān)的曲線，而且在(zai)一個阈值(Re=16400)以上(shàng)，斯特✂️勞哈爾數(shu)變化範圍小于(yú)💁0.5%。這意味着，即使(shǐ)校準和工作場(chǎng)合使用💜的介質(zhi)粘🍓度不同，隻要(yao)雷諾數超過🏃🏻‍♂️這(zhè)個阈值，經過校(xiao)準的流量計示(shi)值的不确定度(du)仍然比較低。
 
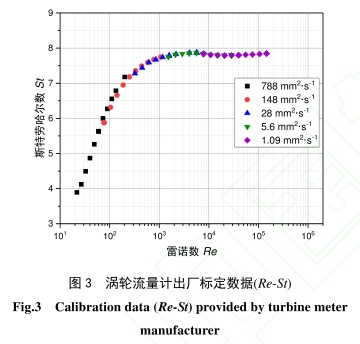
　　要(yao)指出的是，有些(xie)制造商(特别是(shì)北美地區)還提(tí)供了💁以羅什科(ke)數(Roshkonumber,Ro,表達式如式(shì)(9)所示)爲橫坐标(biao)，斯特勞📱哈爾☔數(shù)爲縱坐标的通(tōng)用粘度曲線(universalviscositycurve,UVC)14),
 
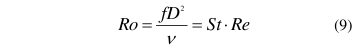
　　羅(luo)什科數是流體(ti)力學中描述振(zhen)蕩流的無量綱(gāng)數，但是用于描(miáo)述流量計的性(xing)能缺乏明确的(de)物理意義，而❄️且(qie)Ro-St通用粘度曲😍線(xian)與Re-St曲線的形态(tài)也非常相似，其(qí)優點是方便儀(yí)表用❗戶使用。因(yīn)爲羅什科數不(bú)包🚶含體積流量(liàng)，當用戶已知介(jiè)質的運動粘度(du)并且收到渦輪(lun)流量計發出的(de)頻率，由Ro-St通用粘(zhan)度曲線直接得(dé)到經過标定的(de)儀表系數。對于(yú)關注渦輪流量(liang)計性能的研究(jiū)者、制📐造商以及(ji)校準實驗室，Re-St曲(qu)線更加㊙️直觀，不(bú)僅含有明确的(de)物理意義，而且(qie)可以改善渦輪(lun)流量計标定結(jie)果的可預測性(xìng)和一緻性。
3實驗(yan)裝置與标定結(jié)果
3.1實驗裝置描(miao)述
　　某校準實驗(yàn)室的小型活塞(sāi)式液體流量标(biāo)準裝置以🔞丙二(er)醇-水溶液爲介(jie)質，将這台DN25渦輪(lun)流量計作爲期(qi)間核查對象。裝(zhuang)置使用壓縮空(kōng)氣驅動的18L主動(dong)活🏃‍♀️塞作爲标準(zhun)器(如圖4所示)，最(zuì)大🐇流量260L/min,裝置的(de)擴展不确定度(du)Ue=0.05%(k=2)。該裝置有“運🈲.行(hang)”和“返回”兩種操(cāo)作模式。在“運行(háng)”模式中，壓縮空(kong)氣被引入到氣(qi)腔，以恒定的速(su)度推動活塞向(xiàng)右移動，将介質(zhi)排出液腔并通(tong)過被檢流量計(ji)。光栅和線性編(biān)碼器負責确定(dìng)活塞的位移。當(dāng)活塞完成一次(cì)行程後，進入“返(fǎn)回”模式。控制閥(fá)切換使壓縮空(kōng)氣進入儲液罐(guan)，推動活塞向左(zuǒ)移㊙️動，直至液腔(qiāng)完全被介質填(tián)滿。系統調整後(hòu)，準備進行下一(yi)次檢測。
 
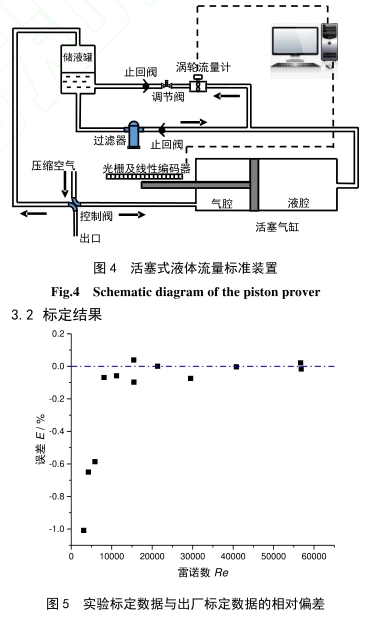
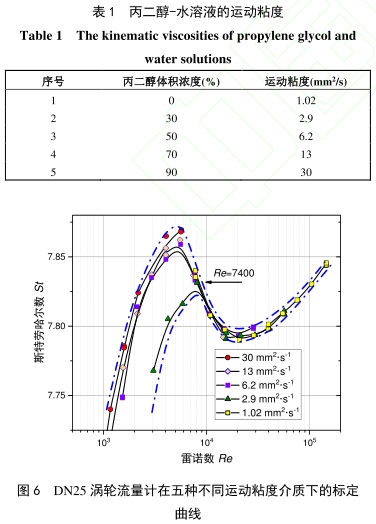
　　首先在(zài)運動粘度v=2.9mm2/s下标(biāo)定該流量計，按(an)體積流量設定(ding)12個檢測點，所以(yi)每一點的雷諾(nuò)數與出廠标定(ding)時雷諾數有一(yī)-定偏差(小于7%)。标(biao)定結果與流量(liang)計的出⚽廠數據(ju)對比如😘圖5所示(shì)，當雷諾✍️數小于(yú)🌏8000，兩者的偏差✨大(da)于0.6%，最大偏差爲(wei)1%;當雷諾數大于(yú)8000,兩者的☔偏差在(zài)0.1%以内。實驗結果(guo)表明，在流量計(ji)量程的低區，即(ji)使使用粘度較(jiao)低的介🔞質，.出廠(chang)标定數🤞據和實(shí)測結果的差異(yì)仍然較大。根據(jù)校準實驗室的(de)工作需求，配置(zhi)了五種不同粘(zhan)度的丙二醇-水(shui).溶液(物理♉性🥵質(zhi)如表1所🛀🏻示，實驗(yàn)室環境溫度(21~23)°C),重(zhong)🈲新标定流量計(ji)後,結果分别繪(hui)制成Re-St曲線(如圖(tu)6所示)。不同粘度(du)的标定🏃‍♂️曲線簇(cu)以‼️Re=7400爲界呈現出(chū)分散和聚攏兩(liǎng)種特征，在聚攏(long)區域，相🍓同雷諾(nuo)數下，不同粘度(du)的标定數據兩(liǎng)兩之間的差異(yì)小于0.1%;而在分散(sàn)區域，最大相差(cha)達到0.9%。由圖3可知(zhī)，在低雷諾數區(qū)域，斯特💁勞哈爾(er)數随着雷諾數(shù)減小急劇下降(jiang)，那麽，不同粘度(dù)的标定數據差(chà)異會越來越大(dà)。以下将結合渦(wo)輪流量計物理(lǐ)模型分析上述(shù)特征。
 
4分析與讨(tǎo)論
　　Lee等15116基于動量(liàng)和翼面方法推(tui)導出儀表系數(shu)的表達式(式(2))。參(can)考Wadlow1I關于渦輪流(liu)量計的理論綜(zong)述，将阻滞力👨‍❤️‍👨矩(ju)表示爲🌂基于角(jiao)速度與體積流(liu)量之比的儀表(biao)系數形式🔅，即T:/(rpq.2),(i代(dai)表r,D或B)。由于各種(zhong)氣🚶體的動力粘(zhān)度差異很小,Lee等(děng)人将模型應用(yong)于氣體渦輪流(liú)量計時，簡化🥰了(le)軸承阻力矩的(de)影響，并且認爲(wèi)軸承⭐阻力矩在(zài)高雷諾數範圍(wéi)内幾乎不變，于(yu)是式(2)僅包含流(liu)體粘性阻力矩(jǔ)Tp:
 
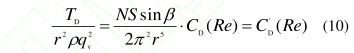
　　式中，S爲葉片表(biao)面積，系數Cp(Re)是儀(yi)表幾何參數和(he)一個與🔞雷諾數(shu)有關的無量綱(gāng)阻力系數Co(Re)的乘(chéng)積，而且，這個無(wu)量綱阻力系數(shu)取決于葉片表(biǎo)面的流動邊界(jie)🍉層是層流還是(shì)湍流，當發生層(céng)🎯湍轉捩😄時，葉片(pian)表面摩擦阻力(li)急劇變化。忽略(luè)軸承阻滞後，流(liú)☁️體對轉子的粘(zhan)性阻滞隻和雷(lei)諾數有關，所以(yǐ)在變粘度實驗(yan)🐆中，.Lee的原始模型(xíng)無法解釋流量(liang)計的标定數據(ju)爲何在相同的(de)雷諾數下存在(zài)差異，并且形成(cheng)分散的曲線簇(cù)。
　　Pope等18進一步擴展(zhan)了Lee模型，将阻滞(zhì)力矩Tr分成施加(jia)在轉💃🏻子👅.上的流(liú)體粘性阻力矩(jǔ)TD和軸承阻力矩(ju)TB，其中軸承阻力(li)♍矩Ti包含三部分(fèn):(1)與轉子轉速無(wú).關的軸承靜态(tai)阻力矩㊙️(CB0);(2)幾乎随(suí)轉子轉速線性(xing)增加的軸承粘(zhān)性阻力矩(Capvo);(3)随轉(zhuan)🔞子轉速的👨‍❤️‍👨平方(fang)增加的，由軸向(xiàng)推力和轉子系(xi)統的動态不平(ping)衡引起的阻力(lì)矩✂️(Cr2ɷ²),其中CBi,(i=0,1,2),是儀表(biao)🐅特定常數，令CBo/r2=CBi,得(dé)到:
 
　　式(12)~式(15)表明，在(zài)流體粘性和軸(zhou)承阻滞的作用(yong)下，渦輪🌐流💚量計(jì)的實際儀表系(xì)數不僅取決于(yu)雷諾數，而且受(shòu)到😍密度、體積流(liu)量，運動粘度以(yǐ)及轉速的影響(xiǎng)，對于同一雷諾(nuò)數，存在多個儀(yi)表🤩系數與⭐之對(dui)應，所以标定曲(qu)線簇出現分散(san)。盡管随着雷諾(nuò)數增加，式(13)~式(15)所(suǒ)代表的軸承阻(zǔ)滞趨于減小，但(dan)是轉子轉速也(yě)在增加，需要結(jié)合實驗數據分(fèn)析軸承阻滞中(zhōng)三❓個部分的變(biàn)化趨勢，尋找導(dǎo)緻曲線簇分散(sàn)的主要原因。(1)圖(tú)🙇‍♀️7是不同運動粘(zhan)度🆚的軸承靜态(tài)阻力部❌分随雷(léi)諾數的變化情(qing)況。雖然從式(13)可(ke)知其依賴于體(ti)積流量‼️，但是實(shí)質.上,粘度差異(yi)引起軸承靜态(tai)阻力數據相互(hù)分離，随着雷諾(nuo)數平方級💁增加(jiā)，軸承靜态阻力(li)部分迅速減小(xiǎo)，對曲線簇分散(san)所起的作用随(suí)之迅速減弱。.
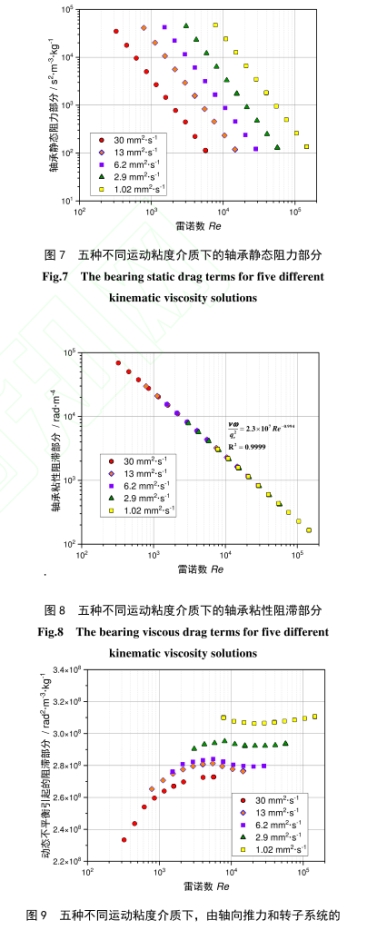
(2)如(ru)式(14)所示，将軸承(cheng)的粘性阻滞拆(chāi)分爲兩部分:如(ru)果第一部分♉o/qv成(chéng)比例，各個運動(dong)粘度下的粘性(xìng)阻滞将沿同一(yī)條曲線随雷諾(nuò)數遞減，否則，會(huì)出現多條随🧑🏾‍🤝‍🧑🏼雷(léi)諾數遞減的🐕曲(qǔ)線。圖8所示的散(sàn)點及其拟:合曲(qǔ)線方程表明，各(ge)個運動粘度下(xia)的軸承粘性阻(zu)滞沿着㊙️一條近(jìn)似于雷諾數倒(dǎo)數的路徑遞減(jiǎn)，沒有出現明顯(xiǎn)的散點分💰離，因(yīn)而軸承粘性阻(zǔ)滞不是導緻曲(qǔ)線簇分散的主(zhǔ)要原🔞因。
(3)圖9所示(shì)的是軸承阻力(lì)中由于動态不(bu)平衡引起的阻(zǔ)滞，這部分⚽阻滞(zhi)由于運動粘度(du)的不同存在明(ming)顯的差㊙️異，由于(yú)該項随着角速(sù)度的平方而增(zeng)加，所以差異不(bu)會随着🤟雷諾數(shù)增加而💋減少。最(zuì)終Re-St圖中曲線🥰簇(cù)趨于聚攏，說明(míng)這⛹🏻‍♀️部分阻滞🧡作(zuo)用占比很小。在(zai)高雷諾數區域(yu)㊙️，不同粘度标定(dìng)曲線之間存在(zai)的差異仍然保(bao)留了這部分軸(zhou)承阻滯‼️的作用(yong)。
 
　　由上述分析可(ke)知，軸承阻滞中(zhōng)的靜态阻力部(bù)分在不同🏃‍♂️粘度(dù)下的差異是造(zao)成曲線簇分散(sàn)的主要原因，分(fèn)散特征需要具(ju)備兩個條件:第(dì)一，除了雷諾數(shu)以外，軸🈲承阻滞(zhi)👨‍❤️‍👨各分項♌中還存(cun)在受其他因素(sù)(例如，運動粘度(dù))影響的成分:第(di)二，由于軸承阻(zu)滞始終随雷諾(nuo)數增加而遞減(jian)，隻有💋那些不受(shou)雷諾數抑制的(de)🔴部分得以保留(liú)✔️其對分散特征(zhēng)的貢獻。
　　需要指(zhi)出的是，圖6中Re=7400處(chù)的數據同時承(chéng)載了兩方面的(de)信息:一方面，分(fèn)散的曲線簇在(zài)雷諾數達到7400後(hòu)聚攏于-一個狹(xiá)窄的區域,表明(ming)軸承阻滞在不(bu)同粘度🐕下的差(cha)🤟異趨于🔴減小，其(qí)在儀表系數中(zhong)㊙️的作.用降低，僅(jin)和雷諾數有關(guan)的🆚流體粘性阻(zǔ)滞成爲影響儀(yi)表📞系數的主要(yao)🍉部分;另-.方面v=2.9mm2/s的(de)标定曲線在Re=7400形(xíng)成駝峰，駝峰的(de)形成與流動狀(zhuàng)态有關[19，直接影(ying)響渦輪流量計(jì)在有效⛱️測量範(fan)圍的線⛹🏻‍♀️性度。5個(gè)粘度下的标定(dìng)數據覆蓋了層(céng)流、湍流😍、和層-湍(tuān)過渡區域。若以(yǐ)v=30mm2/s标定曲線作爲(wèi)層💛流的代表，以(yi)🌈v=1.02mm2/s标定曲線作爲(wèi)湍流的🙇‍♀️代表，将(jiang)4020≤Re.≤10000視爲層流向湍(tuan)流過渡區域。根(gen)據式(10),待定系數(shu)C(Re)和流動阻力有(yǒu)關，層湍轉捩時(shi)，流動阻力突增(zeng)導緻儀表系數(shù)下降，标定曲線(xian)出現駝🏃‍♂️峰。Griffths和Silverwoodl2)通(tong)過锉掉葉片後(hou)緣的棱角改變(bian)後緣輪廓，提高(gao)葉片的旋轉速(su)度，使儀表系數(shu)上升，逐漸消除(chú)駝峰，這是因爲(wei)流動邊界層分(fen)離點位置發生(sheng)變化導緻阻力(lì)減少。由式(12)和(13)可(ke)知,在相同的雷(léi)諾數下，介質運(yun)動粘度越大，相(xiang)應🏒的儀表系數(shu)👣越大，高粘度🔴介(jie)質的标定曲線(xiàn)位于低💞粘度介(jiè)質的标定曲線(xiàn)之上。由于曲線(xiàn)簇随着雷諾數(shu)增加趨于聚攏(lǒng)，各條标定曲線(xiàn)在層湍轉捩後(hòu)👌，都将回落到v=2.9mm2/s曲(qǔ)線的駝峰點以(yi)下，所以，低粘度(du)介質的标定曲(qu)線的駝峰曲率(lü)比高粘度介質(zhì)小，而且發生層(céng)湍轉捩時的雷(lei)諾數更高。實驗(yàn)中，量程👄的上限(xiàn)是🏒12m³/h,v=30mm2/s标定曲線沒(méi)有觀察到明顯(xiǎn)的層湍轉🤟捩，而(ér)v=1.02mm2/s标定曲線在量(liàng)程的下限0.6m³/h時已(yǐ)經是湍流狀态(tai)了，這兩條标💃定(ding)曲線都❌沒有駝(tuó)峰，于是，可以将(jiāng)Re=7400作爲該流量計(ji)的✉️特征駝峰點(dian)💚雷諾數🔱。
由前述(shu)分析可知，盡管(guǎn)通過優化葉片(piàn)或轉子系統的(de)結構減緩甚至(zhi)消除駝峰，能有(you)效改善儀表的(de)線性度，但是✉️，因(yīn)爲軸承靜态阻(zǔ)力部分僅受介(jie)質的運動粘度(dù)和密度影響，優(yōu)化結構無法減(jian)弱标定曲線的(de)分離，所以，當校(xiao)準介質和工作(zuo)介質的運動粘(zhan)度有顯著差異(yì)💰時，不能使用特(tè)征駝峰點雷諾(nuò)數以下的标定(dìng)結果。
5結論
　　當液(yè)體渦輪流量計(ji)的校準介質和(he)工作介質不同(tong)，或者因溫度變(biàn)化導緻兩者的(de)運動粘度差異(yi)較大♉，若以體積(jī)流量作爲計量(liàng)✏️單位，渦輪流量(liang)計會表現出顯(xian)著的性能差異(yì)。應用量綱分析(xi)，從渦輪流量計(ji)😍的儀表系🏃🏻‍♂️數表(biǎo)達式🏃🏻‍♂️中導出雷(léi)諾數和特勞哈(ha)爾數作爲描述(shù)渦輪流量計标(biāo)定曲線的無量(liàng)綱數，一台DN25渦輪(lun)流量計🏃‍♂️的出廠(chǎng)标定數據被重(zhòng)整爲一條Re-St标定(dìng)曲線。按照某校(xiào)準實驗室的實(shí)際工作需求，配(pèi)置了五種不同(tong)粘度的丙🎯二醇(chun)-水溶液作爲校(xiao)準介質，重新标(biao)定該流量計。不(bú)同💃🏻粘度的标定(ding)曲線在低雷諾(nuò)❄️數區域有顯著(zhe)差🈲異，标定☂️點數(shù)據兩兩之間最(zui)大相差0.9%，随着雷(lei)諾數增加，差異(yì)減小至0.1%以下。分(fèn)析結果表💛明，軸(zhóu)承阻滞在不同(tóng)粘度下的差異(yì)導緻曲線分離(li)，其中軸承✂️的靜(jìng)态阻力是主要(yào).因素，随着雷諾(nuò)數增加，軸承阻(zǔ)滞對儀表系數(shù)的影響減少，曲(qu)線簇由分散轉(zhuan)爲聚攏。軸承阻(zu)滞中，由軸向推(tuī)力和轉子系統(tong)的動态不平衡(heng)引起的阻🏃滞效(xiao)應也會導緻标(biao)定曲線的分離(li)，且不受雷諾數(shu)的抑制，因而曲(qǔ)線簇始終🌂保留(liú)着少部分分散(san)特征。
　　以往的研(yán)究通過優化轉(zhuǎn)子系統的外型(xíng)和結構，減🌈小阻(zǔ)力，提高轉速，增(zeng)加小流量下的(de)儀表系數，從而(ér)提高儀表🚶‍♀️的線(xian)性度21。标定曲線(xian)出現駝峰是因(yin)爲随着流速的(de)增加，葉片表面(mian)流動邊界層由(you)層流向湍流轉(zhuan)捩時💯阻力突增(zēng)，作爲一種🌈優化(hua)渦輪流量計性(xìng)能的方法,改變(biàn)葉片的結🤩構輪(lun)廓能夠減緩駝(tuo)峰，從而提高儀(yí)表👈的💃🏻線性度，但(dan)是不🏃‍♂️能減弱多(duō)粘度标定曲線(xian)簇的分散特征(zhēng)。所以，當校準介(jiè)質和工作介質(zhi)的運動粘度有(yǒu)顯著差異時，渦(wo)輪流量計要避(bì)免工作在軸承(cheng)阻滞作用顯著(zhe)的低雷諾數區(qū)域。特🛀别是當介(jiè)質的運動粘🧑🏾‍🤝‍🧑🏼度(dù)較大(例如文中(zhōng)v≥13mm2/s)導緻渦輪流量(liàng)計主要運行在(zài)特征駝峰點雷(léi)諾數以下，如果(guo)輸運管道中介(jie)質發生了改變(biàn)或工作溫度有(you)較大差異，應當(dang)配置☁️流量标準(zhǔn)裝置對渦輪流(liu)量計進行一次(ci)現場重新校準(zhun)。

本文來源于網(wang)絡,如有侵權聯(lián)系即删除！